The geometry incorporated in this study of prehistoric Southwestern architecture makes use of a universal spatial grammar common to both science (Doczi 1981; Kappraff 1991; Lawlor 1995) and art/architecture (Blackwell 1984; Brunes 1967; Doczi 1981; Seymour 1988). The mergence of science and art is a fairly new concept to most Westerners, one that conflicts with our traditional academic separation of disciplines. It appears that this comfortable separation is now coming under fire from some unexpected quarters, such as mathematician Jay Kappraff.

Kappraff makes a case for isolating this geometric standard as a science in its own right through the term design science: "an interdisciplinary endeavor based on the work of mathematicians, scientists, artists, architects, and designers" (1991:xii). In his introduction he cites chemical physicist Arthur Loeb who describes design science as a study of the grammar of space: "spatial structures, whether crystalline, architectural, or choreographic, have their grammar which consists of such parameters as symmetry, proportion, connectivity, stability, etc.; space is not a passive vacuum; it has properties which constrain as well as enhance the structures which inhabit it" (Ibid). Kappraff goes on to explain:

"This book is an exploration of this grammar of space, with the objective to show, by way of demonstration, that this grammar can be the basis of a common language that spans the subjects of art, architecture, chemistry, biology, engineering, computer graphics, and mathematics. Perhaps design science's greatest value lies in its potential to reverse the trend toward the fragmentation resulting from the overspecialization of our scientific and artistic worlds and to alleviate some of the isolation of discipline from discipline that has been the result of that overspecialization" (Ibid).

The practice of "ancient," "secret", "classical," "sacred" geometry was common to many Old World cultures for millennia. It was the geometry of Pythagoras' secret society and Plato's academy (Brunes 1967: 233-258) as it is the philosophical and symbolic staple of modern Freemasonry (Hodson 1976; Hutchens 1988; Singleton 1906). Traditionally, its use and dissemination has developed a mythos of its own (cf. Baigent and Leigh 1994: Chapter 7). The mystical, religious airs associated with this geometrical tradition partly stems from the days of architectural guilds, where only members were introduced to the body of knowledge in order to protect the "tricks of the trade" and thus preserve their livliehood. These pages illustrate some of those tricks, providing solutions to otherwise difficult problems in just a few moments; these problems can range from dividing a circle into three, four, five, six, eight, and ten equal parts to "squaring a circle" - features common to the architecture of Chaco Canyon.

The veneration of this tradition also may be due to its focus on the circle, its radius, and the regular polygons - constructs that mirror Nature's own shapes, forms and proportions (Beard 1973; Critchlow 1970; Doczi 1981; Feininger 1956; Ghyka 1977; Kappraff 1991; Thompson 1969; Wahl 1988). With simple techniques that children can perform, the construction of the perfect shapes from a circle has grand philosophical implications. This operational elegance may be another reason for its enthusiastic reception by young children (Seymour 1988). For Kappraff (1991:xiii): "At a deeper level, ... geometry serves as an intermediary between the unity and harmony of the natural world and the capability of humans to perceive this order."

The geometry is found among many cultures and societies, past and present, from the earliest civilizations of the Near East to modern day logo designers from Madison Avenue. In the Old World, it is found throughout the ancient Middle East and Mediterranean region, especially Egypt, Mesopotamia, Greece, and Rome, and into the architectural and artistic traditions of the modern Christian era ((Blackwell 1984 , Brunes 1967, Hambidge 1924, El-Said and Parman 1976). Brunes (1967, Volume 2: 145-164) applies this geometric system to the structural designs of early Egyptian vases and vessels. It was also common in India (El-Said and Parman 1976), Tibet and China (Lawlor 1995). Not all cultures make the same things with the geometry, but the rules that guide the operations appear fairly universal.

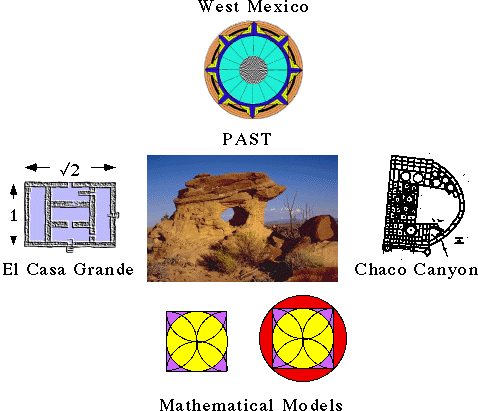
In the New World, the only published indication of its knowledge and practice pertains to the modern Navajo (Pinxten 1987: 39-49; see also Pinxten et al 1983), and the pottery of Zuni and Acoma (Doczi 1981: 23-25); other indications are indirectly evidenced in Zaslow's analysis of iconographic patterns common to Southwestern native cultures (1981; Zaslow and Dittert 1977). Evidence from West Mexico suggests a similar system may have been operating (Weigand 1995, 1996).

Chacoan kivas are stone structures and so lended themselves to relatively precise measurements. Adobe-like structures tend to erode more easily which in turn erodes the possibility for high levels of confidence in extracting those measures. Chaco Canyon also represents an apogee of the Anasazi culture with respect to architectural skills and labor management. If there were design traditions for kivas, they would be best represented in the canyon. Neil Judd's accounts of Pueblo del Arroyo (1959) and Pueblo Bonito (1964), and Gordon Vivian and Paul Reiter's Great Kivas of Chaco Canyon, (1960) were used extensively.

A complex structural tradition like the great kiva contains many elements that can repeat themselves or be replaced over time. Niches, alcoves, ventilator shafts, vaults, postholes and pilasters are among the array of features noted by archaeologists. Size and depth, dates of construction and/or remodelling, and masonry affiliation, are also critical features.

The structures of circular kivas have been discussed and described in a number of reports, though Judd (1959:57-95; 1964: 177-211) and Vivian and Reiter (1960) supplied the critical data for the twenty kivas selected for this examination. The actual reconstruction of a circular kiva was undertaken at Aztec Ruins National Monument where the great kiva was restored on top of the original's ground plan (Tracy Bodnar, personal communication 1998). In another instance, a kiva was built using documentation from archaeological sources (Bruce Bradley, personal communication 1997). One can simply trace a kiva's ground plan and the placement of its floor features, pilasters and so on, and then use the plan to copy a kiva. This practice, however, does not really account for the integrated structural origins of a kiva's features.

Was there an established system behind the designs? If so, can this system be quantified? Two leading scholars on Chacoan architecture, Stein and Lekson (1992:91) are concerned with the overall meaning of the built-form phenomena found in the canyon. "What are the basic parts of the architectural composition and what are the critical issues that organize them?"

"If we are ever to understand Chaco, we must first endeavor to understand the set of "rules" (syntax) that structure the basic architectural vocabulary of the Anasazi-built environment. This is design. A dictionary definition of design is 'the arrangement of parts of something according to a plan.' In contemporary architectural design, building morphology (the design solution) is a mosaic of issues synthesized into the whole" (Ibid:94).

They argue for architectural specialists charged with designing, supervising and sponsoring the efforts (Ibid). "'Image' is a critical function of ritual architecture, and is attained through special techniques that collectively compose a 'sacred technology'" (Stein and Lekson 1992:93).

This examination of the Chacoan kivas provides a systematic method that exposes some of the elements of Anasazi sacred technology in a measurable way. Other examples from Casa Grande, AZ and West Mexico are also provided, suggesting that the geometric system may have a wider currency beyond the boundaries of Anasazi culture.

The analysis of architectural design is confined to the operations of two sticks and a rope (or a peg and stretched rope) when restricted to four very simple rules. The rules limit the options to shapes that correspond with proportional constants. The presence and absence of proportional constants provide: 1) a quantitative context for assessing geometric ratios; and 2) opportunities for reconstructing the techniques that may have generated the architectural designs. The method and the rules that were applied, and the numbers that resulted from this examination, should not be interpreted as a reconstruction of prehistoric mindsets of the architectural designers of these structures. Instead, this exposition of design styles and features is an attempt to invoke Occam's Razor, a popular rule of thumb for scientific endeavors:

Occam's Razor: a scientific and philosophic rule that entities should not be multiplied unnecessarily which is interpreted as requiring that the simplest of competing theories be preferred to the more complex or that explanations of unknown phenomena be sought first in terms of known quantities.

The design solutions are generated from a simple circle with simple tools guided by simple rules. All forms, regardless of aesthetic or symbolic value, are reducible to number and proportion. From these numbers, ratios of internal structural features are available for quantitative analysis. The models presented here are suggested reconstructions of some of those features by a quantifiable, spatial grammar.