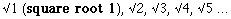
Examining Geometry on its Own Terms. About ten years ago a fundamental riddle in my life was partly answered. I had been wondering why so many cultures, iconographies, religious symbols, corporate logos, and kindergarten classrooms were full of the regular polygons, especially the 60-degree triangle, the square, the pentagon, the hexagon and the octagon. And though I did not include it in my musings at the time: the clock, or dodecagon. In classrooms, one finds them in the forms of blocks, pattern puzzles, the subject of countless coloring and cut-out exercises, and in the string constructs of geo-boards. Therefore the exercises included in this section show how to make these regular polygons from scratch without mathematical requirements. Indeed, many children have accomplished these designs without being able to count to 360. These basic geometric shapes turn up everywhere. Language does not seem to matter. Culture does not seem to matter. They turn up on all continents, in many cultures, and occur with every civilization that has ever risen and passed away. It is as if they are inescapable once you know what to look for. Why is this? What was/is it about them that so consistently attracts the human mind? European - American public education often cites Classic Greece (~500 BC) as the relative origin of geometric appreciation. Yet it was operating in my ancestral lands of western Europe thousands of years before the entity known as Greece existed. The builders of Stonehenge, Avebury, Carnac, Newgrange and other great megalithic projects in neolithic Europe were well aware of these shapes. On the other side of the world, in Prehistoric America, evidence for these geometric shapes turn up in the complex cultures and civilizations of North, South, and Mesoamerica. As investigators become more aware of their presence by recognizing the varieties of their representations and structural origins, it is assured we will find many more instances of their cultural expression, past and present. Known collectively among western culture as "geometric constructions," all the shapes listed above are easily constructed from the circle with the simplest, and thus most elegant, toolkits: on a small scale, the simple compass and any straightedge (such as a ruler); for larger scale constructs, two poles and a rope. The geometry examined at this site is limited to the geometry of the surface plane: a 2 - dimensional geometry where the two dimensions of length and width are theoretically infinite. The third dimension of thickness will not be addressed. The site attempts to serve several purposes. To discuss the nature and the mathematics of the geometry in terms that are required of students through the 9th Grade. To introduce the geometry as a non-random connect-the-dot system grounded by the natural laws of proportion. To furnish a set of rules for both educators and social scientists (including anthropologists and archaeologists) that is easily grasped and easily taught; a set of rules that ensures the preservation of the non-random nature of this type of geometry. To freely provide children and their educators (their parents and their teachers) with an unparalleled learning tool where unlimited art, math and science lessons are discovered woven together in a natural tapestry that dates to Creation. All for the price of a compass, a ruler, some paper, some crayons and other artistic media already present in most schools. When geometry is explored on its own terms, an extraordinary intellectual journey awaits. It begins with two points and is guided by a few self-evident rules and carried out by an economic (cheap) set of tools: a compass for making circles and arcs and a ruler for drawing lines. From this origin, a universe of logical form unfolds non-randomly. Introduced as art to students as young as eight or eighty years, one soon finds that the creative designs are all mathematically logical. The geometry is a science, grounded by physical limitations, reducible to number, and pleasing to the eye. And while students think they're doing art, they will also be doing math and science. You can even add music - Beethoven did. When geometry is pursued in this way, one discovers a method that is best described as connect-the-dots. Because all of the dots (points) are mathematically grounded, one discovers a proportional geometry that ties in concepts required of Middle School and High School curricula, such as pi, phi, Rational and irrational numbers rest side by side in the forms that students will make. It will show them what proportional constants actually look like in their original context. They will use these proportions to make more complex shapes. The physical operations of geometry require only hand-eye coordination. Constructs are made mechanically. No mathematical training is needed. Since all exercises are taught by demonstration, multi-lingual environments will not be an obstacle to teaching. The fact that traditions of non-random geometry were practiced for thousands of years by diverse cultures suggests a logic that transcends linguistic and other cultural variables. As such, non-random geometry could effectively be developed into a multi-cultural standard for assessing intelligence. One of the direct benefits of learning geometry on its own terms is the impact it will have on art programs. Art programs are continuously under fire from local and national quarters that threaten their already weakened budgets. Non-random traditions of geometry are responsible for some of the world's most honored masterpieces, both art and architectural. If geometry could be re-connected with art in national curricula, we could break through the ideological straight jacket that forces us to teach science and art as opposites. It would provide a direct and concrete bridge that ties them together. This "bridge" is not to be thought of as an invented construct, but an objective reality that has been repeatedly discovered over the millennia, and revealed in both art and architecture. The Renaissance was such a period, Chaco Canyon was such a place.